Il blog di Filippo Giordano -

Intervalli quadratici e divisori Mm

Maggio 3, 2024 / filippogiordano

Le chiavi che svelano il segreto della distribuzione dei numeri primi

Fra le adozioni della umanità, nel corso della sua esistenza, l’acquisizione e utilizzo dei numeri naturali interi positivi, a prescindere che essi costituiscano una scoperta o una invenzione, si colloca fra le più antiche seguendo quelle basilari del fuoco, della parola e della scrittura. Nell’antichità, dopo diversi sistemi di contabilità in uso a popolazioni diverse che oscillavano dalla base tre a quella sessagesimale, è infine prevalso l’uso del sistema decimale, che già Aristotele, commentandone l’utilizzo, annotava come naturale trasposizione anatomica del corpo umano stante che nelle nostre mani si contano dieci dita. L’evoluzione di tale sistema, in ultimo con l’ausilio dell’informatica, ha consentito a matematici e fisici di fare realizzare all’umanità passi da gigante. Tuttavia, nell’ambito della mole di tali acquisite conoscenze che i matematici si trasmettono tramite una mole gergale di segni che sintetizza pregresse conoscenze e nuovi concetti, si annida ancora una primitiva lacuna che riguarda la causa della formazione dei numeri primi nel contesto dei numeri naturali. Una lacuna non individuata a causa di una falla che riguarda la mancata conoscenza di una grandiosa proprietà dei numeri naturali i quali si avvalgono di un sistema estraneo a quello decimale disciplinato dall’uomo, ovvero il sistema quadratico che, facendo perno sui quadrati perfetti e su un particolare divisore in dotazione di tutti i numeri naturali, li organizza in infinite “famiglie numeriche” composte di elementi i cui predetti divisori li distinguono in numeri primi, numeri secondi, numeri terzi e così via.

Intervalli quadratici e divisori Mm, chiavi della distribuzione dei numeri primi

I numeri naturali interi si distinguono in primi e composti. La differenza fra gli uni e gli altri consiste nella loro divisibilità. I primi, considerati i mattoni dell’aritmetica, sono divisibili solo per 1 e per se stessi; i composti, oltre che per 1 e se stessi, sono divisibili anche per altri numeri. Ad esempio, il numero primo 11 è divisibile per 1 e per 11 mentre il successivo 12, essendo composto, oltre che per 1 e per 12, è anche divisibile per 2, 3, 4, 6. A differenza dei composti, i numeri primi hanno una distribuzione discontinua, ovvero non prevedibile. A partire dai più piccoli la loro ordinata elencazione consente di esplicitarne l’assunto: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, ecc. Tutti i numeri primi, a parte il 2, sono dispari non multipli di altri numeri. Altra loro caratteristica è la tendenza alla rarefazione. Dei primi cento numeri naturali, i numeri primi costituiscono il 25%; dei primi mille il 16,8%; dei primi diecimila il 12,29%, dei primi centomila il 9,59 e così via scemando. Nel 300 a.C. Euclide dimostrò che nonostante la loro tendenza alla rarefazione essi sono infiniti. Intorno al 1800 il tedesco Gauss e il francese Legendre trovarono una costante di rarefazione, tuttavia, per quanto assiduamente cercata non è mai stata individuata la legge matematica che disciplina la distribuzione dei numeri primi e ciò ha indotto a dubitare che essa effettivamente esista.

Il grande matematico Eulero nel 1721, in proposito, ebbe così a esprimersi: “Ci sono alcuni misteri che la mente umana non penetrerà mai. Per convincersene non dobbiamo far altro che gettare un’occhiata alle tavole dei numeri primi. Ci accorgeremo che non vi regna né ordine né legge”. Marcus du Sautoy, nel suo libro pubblicato nel 2003 ”L’enigma dei numeri primi”, fra l’altro, scrisse: “Come potremo mai riuscire a tracciare un percorso attraverso un tale caos infinito di numeri e a individuare una struttura che ci permetta di prevedere il loro comportamento? (…) Il pensiero laterale, la capacità di rovesciare un problema o di rivoltarlo per vederlo da una prospettiva nuova, è un tema di immensa importanza per le scoperte matematiche”.

Umberto Eco, noto semiologo e filosofo, che in matematica si autodefiniva uno zero, nel 2004, in una sua nota rubrica (Minerva) del settimanale L’Espresso, commentando a suo modo il libro sui numeri primi di Marcus du Sautoy, spinse oltre la sua riflessione: “ … Ora, o la loro successione segue una regola, noi non la conosciamo ma Dio si, e allora tutto andrebbe bene, almeno per Dio. Oppure i numeri primi arrivano davvero a caso, e in tal caso Dio si troverebbe di fronte al Caso, e del caso sarebbe l’effetto, o almeno la vittima non onnipotente (oppure Dio e il caso sarebbero la stessa cosa). Quindi trovare la regola per prevedere la successione dei numeri primi sarebbe l’unico modo per provare non dico l’esistenza ma almeno la possibilità di Dio” e a me che allora vagavo nella oscurità di un totale ateismo, tale riflessione ebbe l’effetto di una molla che mi scagliò alla ricerca dell’interruttore che avrebbe acceso la luce in grado di “non escludere la possibilità di Dio”.

Correva allora, come detto, l’anno 2004. Nei ritagli di tempo del mio abituale lavoro, che niente aveva da spartire con tale l’argomento, nel tempo libero dedicai successivamente parte delle mie amene letture anche allo studio di proprietà note e ignote dei numeri naturali. Lessi, fra gli altri, anche un libro il cui titolo mi incuriosì particolarmente, ovvero: “L’ossessione dei numeri, Bernhard Riemann e il principale problema irrisolto della matematica” scritto da John Derbyshire. In seguito, da qualche parte, lessi una frase del fisico Jhon Wheeler, di certo riferito a qualche altro argomento, che annotai ritenendolo di auspicio: “Un giorno troveremo “la risposta” e saremo sbalorditi della sua semplicità. Un giorno sicuramente vedremo il principio alla base dell’esistenza come così semplice, così bello, così avvincente, che ci diremo tutti l’un l’altro: “come abbiamo potuto essere tutti così stupidi per così tanto tempo? ”

Nel corso della primavera del 2009, studiando la congettura sui numeri primi fatta da Ludwig Oppermann, ebbi una fondamentale intuizione che ritenni risolutrice per la dimostrazione della congettura stessa, la quale, indagata successivamente, a sua volta, si è rivelata sempre più base di partenza di ulteriori scoperte che collimano con la principale proprietà degli intervalli quadratici. Tali ulteriori scoperte da un lato ampliano l’efficacia del metodo di divisibilità di Pierre de Fermat e dall’altro, illuminando un aspetto mai indagato della Spirale di Ulam, mettono in risalto delle ulteriori sorprendenti proprietà dei numeri naturali i quali, osservati con la lente offerta dagli intervalli quadratici e dai suoi particolari divisori, risplendono di nuova luce.

A che mi riferisco e cosa sono gli intervalli quadratici ai quali ho appena accennato ?

Nel suo naturale percorso che da 1 procede verso l’infinito, l’insieme dei numeri naturali interi e positivi si scompone in infiniti sottoinsiemi consecutivi costituiti da coppie di intervalli A e B, limitati e chiusi [n(n-1)+1, n²] e [n²+1, n(n+1)] all’interno dei quali si formano delle “famiglie numeriche” formate da elementi consecutivi, ciascuno dei quali è tendenzialmente caratterizzato da un diverso divisore Mm. Ogni elemento di ciascuna di tali “famiglie” ha un divisore Mm diverso dagli altri elementi che compongono lo stesso intervallo e tutti insiemi formano una compatta squadra i cui divisori Mm formano una scala progressiva che parte dal 1 e arriva sempre alla radice del quadrato perfetto al quale si riferisce ciascuna coppia di tali intervalli.

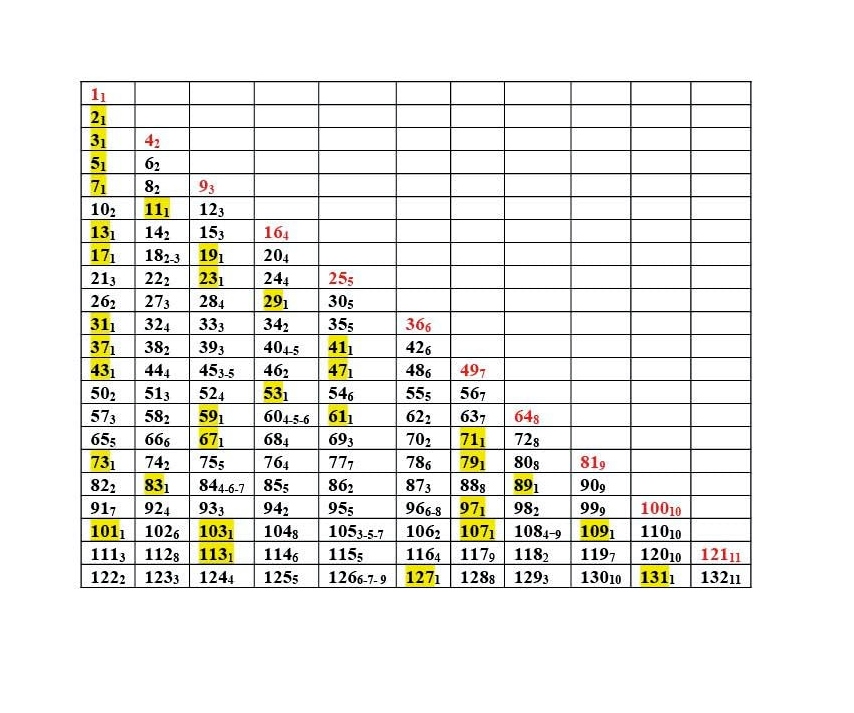
Ad esempio, si consideri l’intervallo A di n=5 composto dai numeri 21, 22, 23, 24, 25 i cui rispettivi divisori Mm sono 3, 2, 1, 4, 5; di n=5 si consideri anche il relativo intervallo B, composto dai successivi 26, 27, 28, 29, 30, i cui divisori Mm sono rispettivamente 2, 3, 4, 1, 5. In entrambi i casi si ha una “famiglia numerica” composta da 5 elementi (quantità uguale alla radice del quadrato perfetto 25, ultimo elemento dell’insieme A) i cui divisori Mm riordinati progressivamente corrispondono a 1, 2, 3, 4, 5, laddove 1 corrisponde al divisore di un numero primo (23 per l’insieme A e 29 per l’insieme B) mentre 5 corrisponde alla radice del quadrato perfetto di pertinenza degli intervalli A (25) e al corrispondente numero oblungo degli intervalli B (30=5×6).

In ciascuna coppia di tali intervalli quadratici, gli elementi dell’insieme A hanno sempre uguale quantità a quelli dell’insieme B, mentre al succedersi di tali intervalli la quantità dei nuovi elementi si accresce sempre di una unità sia nell’insieme A che nell’insieme B, cosicché la naturale quantità di elementi di ciascuna coppia di intervalli A e B, a partire dai primi due intervalli, eccezionalmente costituiti da un solo elemento ciascuno, costantemente si evolve secondo la seguente progressione quantitativa di elementi: 1, 1; 2, 2; 3, 3; 4, 4; 5, 5; …, n, n; Tale evoluzione della quantità degli elementi di ciascun intervallo che comprende tutti i numeri naturali da 1 all’infinito, nessuno assente e nessuno ripetuto, comprende sempre, quale ultimo elemento di ciascun intervallo A, un nuovo quadrato perfetto il cui pertinente valore della radice determina la quantità dei numeri naturali degli insiemi A e B, così come si evince dal seguente iniziale prospetto:

01 – 02;

03, 04 – 05, 06;

07, 08, 09 – 10, 11, 12;

13, 14, 15, 16 – 17, 18, 19, 20;

21, 22, 23, 24, 25 – 26, 27, 28, 29, 30;

31, 32, 33, 34, 35, 36 – 37, 38, 39, 40, 41, 42;

43, 44, 45, 46, 47, 48, 49 – 50, 51, 52, 53, 54, 55, 56.

Tale organizzazione prevede la corrispondenza biunivoca di gruppo tra quantità di elementi degli intervalli e quantità dei loro divisori Mm (acronimo di Maggiore dei minori) che coprono l’intera scala compresa fra 1 ed n, cosicché, ad esempio, il corrispondente divisore Mm della prima coppia di intervalli costituita da 1 e 2, è 1, 1 in quanto entrambi divisibili solo per 1 e per sé stessi; i corrispondenti divisori Mm della seconda coppia di intervalli (3, 4 e 5, 6) sono 1, 2, e 1, 2; i corrispondenti divisori Mm della terza coppia di intervalli (7, 8, 9 e 10, 11, 12 sono 1, 2, 3, e 2, 1, 3; i corrispondenti divisori Mm della quarta coppia di intervalli (13, 14, 15, 16 e 17, 18, 19, 20 sono 1, 2, 3, 4, e 1, 2-3, 1, 4. Pertanto ad ogni intervallo A e B composto da n elementi corrisponde sempre un intervallo di n divisori Mm i cui valori sono compresi fra 1 ed n.

Ogni qualvolta qualche elemento dell’intervallo accentra su di sé più di un divisore Mm, tale confluenza di divisori Mm nel medesimo elemento numerico è causa, nello stesso intervallo, della replica di elementi il cui divisore Mm è MCD dei divisori Mm confluenti. Ad esempio, nell’intervallo B dello stesso n=4, composto dagli elementi 17, 18, 19, 20, poiché l’elemento 18 è contemporaneamente divisibile sia per 2 che per 3, fra loro primi, allora, poiché MCD di 2 e 3 è il numero 1, la confluenza dei due divisori 2 e 3 sull’elemento 18, stante che il loro MCD è 1, diviene causa della replica di un elemento di uguale divisore il che, in tale intervallo, comporta la presenza di due numeri primi. Infatti, i divisori dei quattro elementi di tale intervallo sono 17=1; 18=2, 3; 19=1; 20=4, ovvero intervallo contenente la presenza di un elemento con due divisori Mm fra loro primi che causa la doppia presenza di numeri primi nel contesto dello stesso intervallo.

Tale “naturale” dinamica matematica (provvista di una serie di regole uniformemente applicabili a tutti gli intervalli) è quindi causa di almeno un numero primo per ciascuno degli intervalli A e B iniziali e, col costante aumentare della quantità di elementi contenuti negli intervalli man mano che cresce il valore di n, diviene causa di una frequente crescita di numeri primi all’interno degli intervalli medesimi. Tale dinamica matematica spiega perché nei 10 elementi dell’intervallo A che fanno riferimento al quadrato perfetto 100 [91, 100] si trova un solo numero primo mentre nei 10 elementi successivi [101, 110] che costituiscono il pertinente intervallo B se ne trovano 4. La stessa dinamica matematica spiega anche perché, a partire da n=4, in tutti gli intervalli B di n pari esistono sempre almeno due numeri primi: [17, 20; 37, 42; 65, 72; 101, 110; 145, 156; …]

Maggiore è la quantità di tali tipi di confluenze di divisori negli intervalli, maggiore è la presenza dei numeri primi. Basti pensare che mentre entro le prime 17 coppie di intervalli la quantità dei numeri primi in essi contenuti oscilla fra 1 e 4, già a partire da n=18 ciascun intervallo A e B, contiene sempre almeno due numeri primi. In ogni caso, qualsiasi sia il valore di n, esiste sempre la corrispondenza biunivoca fra quantità di elementi e distribuzione di divisori Mm che sempre copre l’intera gamma di valori compresi fra 1 ed n, laddove gli estremi [1, n] rappresentano 1= divisore Mm dei numeri primi ed n radice del rispettivo quadrato perfetto. Grazie al metodo di divisibilità individuato da Fermat, opportunamente esteso, da ciascuno di tali intervalli si ricavano sempre alcuni divisori Mm che consentono la subitanea individuazione di alcuni elementi sicuramente composti mentre con un metodo suppletivo si vanno ad individuare tutti gli altri elementi composti rimanenti dell’intervallo. Perennemente, gli elementi residui di tali crivelli isolano ed individuano sempre i restanti elementi quali numeri primi.

Considerate le precise regole di individuazione gerarchica di tutti gli elementi composti di ciascun intervallo è, sempre possibile, tramite l’ausilio di un eventuale programma informatico appositamente predisposto, individuare celermente negli elementi residui i sicuri numeri primi appartenenti a ciascun intervallo. Tuttavia, poiché ciascuna coppia di intervalli quadratici A e B fa riferimento a un diverso quadrato perfetto, essendo il valore di ciascuna radice ovviamente diverso da tutti gli altri, e dovendosi strutturare la ricerca degli elementi obbligatoriamente secondo il valore gerarchico dei divisori Mm (partendo dal valore più alto e proseguendo gradualmente verso il basso fino al valore 2), essendo perennemente diversa la quantità degli elementi di ciascuna coppia di intervalli dalle altre coppie, si verifica una frequente alterazione delle postazioni assunte dagli elementi residui dei numeri composti e ciò implicitamente determina una frequente alterazione di posizione dei numeri primi all’interno degli intervalli quadratici. Il che impedisce che possa esistere una formula univoca che consenta di estrapolare dal contesto dei numeri naturali tutti i numeri primi.

Il fatto che la presenza dei numeri primi all’interno degli intervalli quadratici tenda ad aumentare (si consideri in proposito che quando n assume il valore n = 20.000 i numeri primi presenti nel pertinenti intervalli A e B corrispondono rispettivamente a 1029 + 986, il che equivale alla quantità di confluenze di divisori Mm presenti negli stessi intervalli) non è una contraddizione bensì un naturale freno alla rarefazione; un freno che se non esistesse, ridurrebbe drasticamente l’effettiva quantità dei numeri primi rispetto ai composti, sia pure conservando la loro onnipresenza all’interno degli intervalli, e renderebbe estremamente semplice il calcolo della quantità dei numeri primi (sempre uno per ciascun intervallo, così come succede per le primissime coppie di intervalli).

Tale naturale struttura distributiva dei divisori Mm all’interno degli intervalli quadratici dei numeri naturali interi positivi che garantisce sempre la presenza di almeno due numeri primi fra ciascun quadrato perfetto e il suo successivo (almeno uno per ciascun intervallo A e B), stante che i quadrati perfetti non hanno mai fine, dà “corpo” alla astrazione del teorema euclideo che, nonostante la tendenza alla rarefazione, assicura e garantisce l’infinita presenza dei numeri primi essendo naturale la loro presenza all’interno di ciascun intervallo quadratico A e B.

Al contempo, la stessa semplicità concettuale delle altalenanti confluenze dei divisori Mm nei numeri naturali composti compresi negli intervalli quadratici che determinano il ritmo sincopato dei numeri primi, considerato che non esistono ulteriori ragioni matematiche che possono variarne il flusso, induce a dedurre che la rarefazione dei numeri primi rimarrà costante nella misura quantificata da Gauss anche nelle regioni matematiche ignote e pertanto la eventuale dimostrazione della ipotesi di Riemann non potrà che risolversi positivamente.

III

Intervalli quadratici e divisori Mm, chiavi della distribuzione dei numeri primi

Riflettendo sulla dinamica matematica assunta dagli elementi e dai pertinenti divisori Mm degli intervalli quadratici penso che, essendo i numeri primi essenza che costituisce la base della evoluzione matematica, la loro asimmetrica distribuzione nel contesto dei numeri naturali nasconde una regola talmente elementare da potersi considerare primordiale. Una base dalla quale i moderni discepoli di Euclide, a causa della continua evoluzione di segni e concetti in uso alla matematica moderna, si vanno sempre più allontanando, rendendo così sempre più remota la possibilità di un aggancio dell’edificio matematico con le sue fondamenta.

Già da diversi decenni, fra gli esperti di analisi matematica vige la diffusa convinzione che poiché i grandi matematici del passato ai loro tempi hanno “sicuramente” percorso tutti i semplici sentieri possibili senza approdare alla soluzione del dilemma relativo alla distribuzione dei numeri primi, si deduce che non esiste una soluzione semplice del problema e tale errata convinzione pregiudica il loro rapporto con qualsiasi ricerca elaborata in forma elementare, imperando la pseudo certezza che l’agognata soluzione possa essere offerta solo e soltanto risolvendo l’ipotesi di Riemann del 1859; soluzione, peraltro, da allora invano cercata e nonostante empiricamente avallata, da madre Natura non offerta ai matematici che vi si sono cimentati. Tale convinzione sembra essersi accentuata a seguito della complessa soluzione matematica offerta nel 1994 dal matematico inglese Andrew Wiles relativamente al quesito posto dal cosiddetto “ultimo teorema di Fermat” matematico “per diletto” vissuto nel corso del XVII secolo.

Di tale mia supposizione, ho acquisito convinzione quando, dopo avere notato l’effetto sorprendente del citato divisore Mm,pian piano ho trovato con essa agganci con idee appartenenti a tre matematici del passato: Oppermann, Fermat e Ulam (agganci che di volta in volta sono serviti da base di partenza per estendere la loro ricerca in altre direzioni che arricchiscono le loro originarie idee). Idee diverse che, debitamente sviluppate, convergono nella unica direzione degli intervalli quadratici da me individuati. Aggiungo inoltre che la dinamica matematica che si sviluppa all’interno degli intervalli quadratici tramite corrispondenza biunivoca tra elementi e loro divisori Mm dimostra fondata e vera la congettura del matematico romeno Dorin Andreca riguardante gli intervalli tra due successivi numeri primi, così come chiunque potrà convenire dopo averne acquisito conoscenza.

Sicché, ritengo che finalmente l’infinito albero dei numeri naturali consente di guardare l’esatta consistenza del suo apparato radicale. Tale visione dell’oltre mi consente di affermare con piena convinzione che esiste una particolare disposizione di coppie di intervalli, a cui sono soggetti tutti i numeri naturali, il cui effetto latente (derivante dalla sostituzione degli elementi numerici compresi negli intervalli coi loro singoli divisori Mm) è specchio sublime di una intrinseca proprietà dei numeri naturali. Una disposizione affatto casuale, bensì rivelatrice di un celato sottordine dei numeri naturali armoniosamente disposti in un virtuale geometrico triangolo.

Un triangolo i cui minuti elementi disposti a spirale, seguendo l’originario grafico di Ulam, si trasforma in un quadrato che si espande nelle quattro direzioni cardinali e, reinterpretato seguendo la logica matematica degli intervalli quadratici, mostra un meraviglioso infinito numerico equamente distribuito in quattro triangoli ciascuno dei quali ospita ininterrotte sequenze di intervalli quadratici di uguali caratteristiche, ovvero intervalli quadratici A di n dispari, intervalli quadratici B di n dispari, intervalli quadratici A di n pari, intervalli quadratici B di n pari. Quattro triangoli, i cui vertici confluiscono al centro, da ciascuno dei quali si dipartono scie di divisori Mm che si distribuiscono verso l’esterno in ordinate e ininterrotte sequenze.

Così come, leggendo, dal linguaggio utilizzato certamente si è già capito, per fortuna dei numeri primi che erano stufi di essere da sempre vissuti da incompresi, chi scrive non è un matematico tradizionale, bensì, un modesto amante della Natura, della Musica, della Poesia e delle Proprietà note e ignote dei Numeri Naturali, curioso di scoprire e assimilare le loro proprietà, ovvero un dilettante detective, auto prestatosi alla ricerca delle armonie recondite insite nella Natura.

Quando, intorno al 2002, studiando i fenomeni ciclici dei numeri naturali risolsi il dilemma del perché tutti i numeri perfetti hanno radice numerica sempre uguale a 1… cominciai a chiedermi se “per caso” anche i numeri primi potessero avere una qualche attinenza con tale fenomeno ma, essendo la problematica relativa alla distribuzione dei numeri primi molto più complessa, inizialmente non trovai niente di soddisfacente in tale direzione. Fu soltanto diversi anni dopo avere compreso la grande proprietà dei numeri naturali insita negli intervalli quadratici (con annessi fenomeni delle convergenze dei divisori Mm su alcuni elementi che implicitamente causa la replica sistematica dei numeri primi negli stessi intervalli) che trovai ciclicamente disposti, dentro analoghe tipologie di intervalli quadratici, alcuni di quegli elementi composti che ospitano divisori Mm fra loro primi (i quali sempre sono sempre causa delle repliche dei numeri primi) il che consente di dimostrare la perpetua presenza dei numeri primi dentro ciascun intervallo quadratico. Ma la sostanziale differenza fra i due fenomeni di ripetizione ciclica di numeri naturali fra numeri perfetti e numeri primi è che nel primo caso mi sono bastate solo tre pagine per la dimostrazione mentre nel secondo ne sono occorse diverse decina.

La stesura finale del libro a cui ho dato il nuovo titolo di “Intervalli quadratici e divisori Mm, la disciplina dei numeri naturali che regola la distribuzione dei numeri primi” è un volume di 230 pagine di formato A4, che comprende molteplici tabelle esplicative delle quali 30 a colori “Intervalli quadratici e divisori Mm, la disciplina dei numeri naturali che regola la distribuzione dei numeri naturali”. Il nucleo portante della teoria è corredato da diversi approfondimenti collaterali che affrontano molteplici aspetti, compresa, in coda, la spiegazione dettagliata dei movimenti “robotici” dei divisori Mm all’interno delle prime quindici coppie di intervalli.

A conclusione di questa introduzione osservo che essendo i numeri primi “essenza” che costituisce il punto di partenza per la comprensione delle basilari proprietà dei numeri naturali, la comprensione della loro asimmetrica distribuzione nel contesto dei numeri naturali costituisce una fondamentale tappa per l’evoluzione della matematica e a tal proposito osservo anche che una interpretazione elementare, quale è quella degli intervalli quadratici, assecondi meglio l’orientamento dello “Spirito” primordiale dei numeri naturali, stante che l’ordinamento decimale concordato dalla umanità per comodità di calcolo, invece, non ne consente di afferrarne la dinamica.

D’altronde, dal mio punto di vista, rilevo che questa mia teoria degli intervalli quadratici non è da intendere come una evoluzione della matematica moderna bensì come sua base, essendo l’edificio matematico che ospita i numeri naturali finora sospeso su un vuoto culturale che ha sempre lasciata insoddisfatta la domanda: “Esiste una legge matematica che regoli la distribuzione dei numeri primi?” Una base sostenuta da ragionamenti matematici elementari che, per tale specifico motivo, avrebbe potuto benissimo essere colta da una delle qualsiasi brillanti menti matematiche che si sono succedute nel corso dei secoli, non essendo necessario per la sua dimostrazione ricorrere alle moderne evoluzioni del “matematichese”, bastando fare una regressione quale è quella del sistema degli intervalli quadratici utilizzati dalla Natura.

A corredo e supporto dello studio dei numeri primi lungo il corso degli anni di evoluzione della basilare scoperta degli “intervalli quadratici” fra le cui proprietà è compresa quella della dinamica aritmetica della formazione dei numeri primi, al fine precipuo di stabilire eventuali connessioni tra il noto e l’ignoto, nel tempo ho eseguito uno studio parallelo su diversi altri aspetti dei numeri naturali interi positivi. Sicché, nel corso degli anni, anche al fine di conservarne memoria personale, ho fermato in una personale collana le seguenti pubblicazioni mono-tematiche:

Primi di Mersenne e numeri perfetti. Esplorazione di una rarità numerica. Edizione Youcanprint 2013, successivamente ampliata ed elaborata in formato più grande (21×30) al fine di una più agevole lettura delle pagine contenenti specifiche tabelle, nel 2022, sempre coi tipi della Youcanprint.
Terne pitagoriche primitive. Edizione Youcanprint 2013, anch’essa successivamente riveduta in formato più grande (21×30) al fine di una più agevole lettura delle pagine contenenti specifiche tabelle e riedita nel 2022.
Spirale di Ulam, la straordinaria mappa dei sottordini dei numeri naturali che regolano la distribuzione dei numeri primi, edizione Youcanprint 2013, anch’essa successivamente ampliata in formato più grande (21×30) e riedita nel corso del 2020 sempre coi tipi della Youcanprint.
Rette numeriche quadratiche, le impalcature matematiche che guidano la fattorizzazione dei numeri naturali, formato 21×30, Youcanprint 2021.
Progressioni aritmetiche di numeri primi, formato 21×30, Youcanprint 2022.
Fattorizzazione dei numeri naturali, evoluzione del metodo di Fermat e nuove scoperte, formato 21×30, Youcanprint 2023.
Quaterne quadratiche, terne pitagoriche, primi gemelli e altre ricerche e dissertazioni sui numeri naturali, formato 21×30, Youcanprint 2023.

Per saperne di più clicca su “leggi l’estratto” alla pagina libro che si apre sul sito di Youcanprint

https://store.youcanprint.it/intervalli-quadratici-e-divisori-mm-la-disciplina-dei-numeri-naturali-che-regola-la-distribuzione-dei-numeri-primi/b/ac83aad3-1809-5c8c-bef8-93f418269008

Sussurri del cielo e mormorio di numeri primi

Settembre 12, 2024 / filippogiordano

Alcune poesie del libro

“Sussurri del cielo e mormorio di numeri primi”

NATALE

Vago lo sguardo nell’immenso cielo

sperando nella scia delle comete.

Straripa a volte il Caso dilagando

fra meteoriti che cozzano pianeti

nei loro lunghi viaggi senza meta,

pietra scagliata sulla carne inerme

che si contorce e spasimando implode

polverosa concime della terra.

È l’uomo figlio d’uno scriteriato

ordine di forze che s’attraggono

o collima la sua intelligenza

ansiosa con il Tuo volere?

Chi sono i puri ai quali Tu concedi

il codice che valicando il dubbio

nutre di fede il corpo e l’esistenza?

È gonfio di silenzi il Tuo respiro …

oppure parli una lingua universale

di planetarie geometrie elicoidali

numeri primi, quadratiche distanze

fra ognuno di loro e i suoi discenti,

moti (e sommovimenti della mente)

infiniti, che il pensiero racchiude?

°°

Prima del principio era lo zero

Prima del principio era lo zero.

Un assoluto vuoto di pensiero.

Poi venne il soffio dello Spirito

ad animare di pulsante linfa

la materia oscura e senza tempo.

Soffiò la vita e l’uomo venne,

solitaria creatura intelligente

fra animali e piante d’ogni specie

a far tesoro della esperienza

delle somme dei cicli di stagioni.

Il soffio magico regolò la vita

secondo un disegno preordinato

di cicli naturali susseguenti.

Ciclo di terrestre rotazione

attorno al sole,

cicli di rotazione dei pianeti,

ciclo lunare, ciclo dominicale,

ciclo mestruale, ciclo di stagioni,

ciclo di esistenza delle piante,

alberi, animali e, dulcis in fundo,

il ciclo di esistenza degli umani.

°°°

Masse di cicli

Masse di cicli chiusi ma gravidi

di semi per cicli successivi;

cicli chiusi eppure aperti cicli

che inseminandosi l’un l’altro

allungano come anelli di catena

il tempo sotto il cielo azzurro

di storie umane e loro contorni.

Cicli di lezioni matematiche

con armoniche cadenze di tempo

che aprono e chiudono pagine

del grande libro mastro della terra;

manuale della sinfonia stellare

che l’uomo sogna di decodificare.

Perenni cicli di numeri primi

alla corte dei numeri quadrati

integerrimi e onnipresenti

cavalieri di perpetue, ricorsive

e progressive scuderie numeriche.

°°°°

Dio è sorgente di luce che abbaglia

Dio è sorgente di luce che abbaglia

tanto intensamente da impedire

la diretta visione dello Spirito;

così soltanto la riflessa luce

che Egli emana

indirettamente a Lui conduce

e tuttavia il mentale viaggio

a ritroso è possibile solo

credendo intensamente che il riflesso

che di luce abbaglia –

abbia una fonte dove essa sgorga.

Dove e quando lo Spirito sussurra

all’uomo il suo ordine velato

quel frammento di luce rilasciata

che travasa dentro il corpo

come fulminea scia

un attimo congiunge alla sorgente

lo spirito vivo all’eterno Spirito.

Cenni sulla teoria della formazione dei numeri primi

(nota dell’autore, in appendice del libro)

A un certo punto della propria storia, per comodità di calcolo l’uomo inventò il sistema decimale. La tavola pitagorica, appresa alle elementari, elaborata dentro un quadrato di cento caselle in ognuna delle quali stanno i numeri da 1 a 100, penso che sia nella memoria di tutti. Essa, riflette, sinteticamente, uno dei molteplici metodi dell’uomo per semplificarsi la vita. La metodica del sistema decimale, entrata nella forma mentis della civiltà umana, non ha però consentito di decifrare l’enigma della regola di distribuzione che seguono i numeri primi all’interno dei numeri naturali.

Dio, o, se volete, la Natura, ha pensato alla distribuzione dei numeri in forma diversa. Attenzione: non mi riferisco alle regole matematiche e neanche al naturale succedersi dei numeri. Dico solo che per comprendere il meccanismo matematico che regola la distribuzione dei numeri dobbiamo pensare a una disposizione diversa da quella decimale. Col sistema decimale, inventato dall’uomo, l’altalenante flusso dei primi nel contesto dei numeri naturale appare slegato da qualsiasi regola. Non c’è alcuna formula matematica che sia in grado di potere preventivare la loro apparizione. Non c’è modo alcuno di potere stabilire come e perché a sporadiche presenze succedano, talvolta, presenze più compatte. Dal numero 90 al 100 c’è un solo numero primo. Dal numero 100 al numero 110 ne troviamo, invece, 4. Un bel rompicapo che per oltre duemila anni ha tenuto in scacco i matematici di tutto il mondo. Nel 1751, in proposito così si espresse il grande Eulero: “Ci sono alcuni misteri che la mente umana non penetrerà mai. Per convincersene non dobbiamo far altro che gettare un’occhiata alle tavole dei numeri primi. Ci accorgeremo che non vi regna né ordine né legge.”

Dopo il teorema di Euclide, che nel 300 a.C. riuscì a dimostrare che i numeri primi sono infiniti, il più grande progresso ottenuto dai matematici su questo specifico settore della matematica fu conseguito dal tedesco Gauss che intorno al 1800 riuscì empiricamente a quantificare, con una formula approssimativa, in che proporzione i numeri primi sono presenti rispetto a tutti gli altri numeri. Poi, nonostante negli ultimi 60 anni grandi elaboratori delle facoltà di matematica del mondo siano tesi alla ricerca di sempre nuovi numeri primi, le cui dimensioni sono mastodontiche, tanto che per scriverne solo uno ci vogliono libri di diverse centinaia di pagine, non si è ottenuto alcun significativo progresso utile a decifrare l’alone di mistero che circonda la nascita dei numeri primi. Dopo essere venuto a conoscenza della problematica, da dilettante appassionato della materia, ho approfondito il problema. Lungo il tragitto degli studi effettuati in proposito ho avuto modo di comprendere altre problematiche connesse ai numeri primi, riuscendo ad elaborare un teorema relativo ai numeri perfetti, entità numeriche che ai primi sono strettamente collegati, che risolve un antico enigma matematico. Cenni su tale teorema sono stati pubblicati su una tesina sui numeri perfetti pubblicata sul sito internet della Università di Torino, sulla pagina personale della allora docente, fintanto che la stessa è andata in quiescenza.

Ma, visto che il sistema decimale, in uso nella nostra civiltà, ha impedito a fior di matematici di decifrare il segreto dei numeri primi, qual è l’altro sistema che consente di venire a capo del problema della distribuzione dei numeri primi?

II sistema quadratico. Ma cos’è il sistema quadratico? Se solo ora venite a conoscenza di tale definizione … state tranquilli! Non si tratta di una vostra particolare lacuna culturale poiché essa è frutto di una mia originale interpretazione della distribuzione dei numeri interi e naturali. Un particolare modo di disporre i numeri, non ancora codificato dalla scienza matematica, che il Padreterno ha tenuto in serbo per tanto tempo, riservandosi di rivelarlo alla nostra generazione, per il tramite del più semplice fra i matematici, non provvisto di specifico titolo e perciò lontano dai sentieri normalmente percorsi da chi il titolo ce l’ha, un matematico semplice tuttavia provvisto di un’altra semplice grazia: quella della fantasia immaginativa; grazia concessa ai poeti, sia pure non di grido.

Perché fantasia immaginativa e semplicità, con l’aiuto di Dio, talvolta riescono a trasformarsi in pensiero laterale, ovvero capacità di individuare sentieri primitivi coperti dalla moderna e lussureggiante vegetazione di formule sempre più sofisticate. Sentieri primitivi attraverso i quali è possibile, che uno squarcio di luce pazientemente cercato faccia capolino e, dopo avere scostato l’ultima fronda, ti accolga nella sua rasserenante verità.

Di questo, dunque, parlo in questo libro dal linguaggio arcaico, lontano dal “matematichese” moderno, che descrive origine e funzione dei numeri primi nel contesto della distribuzione dei numeri naturali: del sistema quadratico: concetto di distribuzione numerica semplice da assimilare. Distribuzione numerica che contiene al proprio interno i codici gametici dei numeri, cioè le coppie di fattori che formano i numeri stessi. Un fenomeno che, correttamente inquadrato, si dimostra perpetuamente fedele. Un fenomeno concreto, tangibile e reale, valido per tutti gli insiemi numerici consecutivi, strutturalmente identificati, che consentono di prendere piena coscienza della dinamica matematica che fa scaturire i numeri primi.

Un fenomeno che da sé stesso ha forza auto dimostrativa, ma che io, successivamente alla prima stesura, ho supportato con altre integrazioni riuscendo a consolidare la teoria oltre che con la prova empirica anche con la dimostrazione matematica; dimostrazione che ancora una volta si affida ai cicli numerici dei numeri per la lettura della quale, essendo elaborata su diverse decine di pagine, rimando alla ultima stesura del libro stesso che ha titolo “Intervalli quadratici e divisori Mm, la disciplina dei numeri naturali che regola la distribuzione dei numeri primi, volume di 230 pagine edito tramite Youcanprint nel corso del 2024. Di seguito, invece, mostro l’originale idea, successivamente sviluppata su diversi fronti tematici che ne confermano la corretta intuizione, che ha consentito di imboccare il giusto percorso che conduce alla soluzione.

Immaginate la sequenza dei numeri naturali, che partendo dall’1 arriva all’infinito, disposta a coppie di insiemi numerici omogenei A e B (detti intervalli) lungo delle linee orizzontali. Immaginate che le caratteristiche costanti di tali insiemi omogenei siano che ogni linea orizzontale contenga una serie di numeri consecutivi il cui ultimo elemento coincide sempre con un quadrato perfetto e che la quantità di tali elementi sia sempre corrispondente alla radice del quadrato perfetto di riferimento (ad esempio: elementi 21, 22, 23, 24, 25, dei quali è quadrato perfetto il 25, la cui radice è 5, quantità che corrisponde al totale di elementi di tale insieme, che definiamo intervallo A). Nello stesso rigo, immaginiamo un secondo gruppo di numeri consecutivi costituito da uguale quantità di numeri consecutivi, successivi al primo, ovvero 26, 27, 28, 29, 30, che definiamo intervallo B. Tali coppie di insiemi numerici sono rispettivamente catalogabili quale intervallo limitato e chiuso [n(n-1)+1, n²], corrispondente all’intervallo A, nonché [n²+1, n(n+1)] corrispondente all’intervallo B. La ordinata successione delle prime coppie di tali intervalli numerici corrisponde alle seguenti:

01 – 02

03 – 04 – 05 – 06

07 – 08 – 09 – 10 – 11 – 12

13 – 14 – 15 – 16 – 17 – 18 – 19 – 20

21 – 22 – 23 – 24 – 25 – 26 – 27 – 28 – 29 – 30

31 – 32 – 33 – 34 – 35 – 36 – 37 – 38 – 39 – 40 – 41 – 42

In ogni linea si formano due insiemi di numeri consecutivi che rispettivamente corrispondono all’Intervallo quadratico A, l’ultimo elemento dei quali, alternativamente dispari e pari, corrisponde sempre all’ennesimo quadrato perfetto, e all’intervallo quadratico B, il cui ultimo elemento, sempre pari, corrisponde al numero oblungo sempre uguale a n(n+1).

Il numero degli elementi di ciascuno dei due insiemi, come detto, è sempre uguale alla radice del quadrato perfetto di riferimento. Supponendo che per n si intende quel numero di partenza che si è elevato al quadrato, è facile calcolare che se n = 4, il suo quadrato è uguale a (4×4) = 16 e che il numero degli elementi dei due insiemi A e B è formato da n elementi, cioè 4, precisamente il 13, 14, 15, 16 per l’insieme A e 17, 18, 19, 20 per l’insieme B.

Dopo questa premessa ne facciamo una seconda.

Tutti i numeri interi e naturali risultano essere prodotti di coppie di fattori. I numeri primi sono sempre il prodotto di una sola coppia di fattori, cioè il numero 1 e il numero stesso. Ad esempio, il numero 7, che è numero primo, è il prodotto di 1 x 7. Quindi il 7 è prodotto dell’1 che moltiplica lo stesso 7.

I numeri composti sono prodotti da 2 o più coppie di numeri. Ad esempio: il numero 10, che è numero composto, risulta essere il prodotto della coppia 1 x 10 ed inoltre dalla coppia 2 x 5. Il numero 9, che è pure composto ed è il quadrato di 3, risulta essere il prodotto della coppia 1x 9 e della coppia 3 x 3 (cioè un numero che moltiplica sé stesso). Quindi le coppie di fattori dai quali ciascun numero è prodotto, sono uguali se esso è un numero quadrato.

Posto che n = 5, allora il numero 25 è prodotto di 2 fattori uguali, cioè n x n, ovvero 5 x 5, mentre il numero oblungo, costituito dall’ultimo elemento dell’intervallo B è uguale 5×6. Ad eccezione del quadrato perfetto e del corrispondente numero oblungo, preso un altro numero qualsiasi appartenente alla stessa linea di n = 5, esso risulta sempre costituito da due fattori di cui uno inferiore e l’altro superiore a n. Ad esempio, il numero 21 è prodotto di 2 fattori diversi fra loro (3×7) di cui uno inferiore a 5 e l’altro superiore a n (3×7).

Quindi gli elementi numerici che si trovano lungo questa linee orizzontali hanno la caratteristica ovvia di avere coppie di fattori uguali a n per l’elemento quadratico (5×5=25) e ad n(n+1) per l’elemento oblungo (5×6=30), mentre tutti gli altri elementi hanno coppie di fattori di cui uno è inferiore a n e l’altro è superiore. L’elemento 22, ad esempio, oltre che essere il prodotto della coppia 1×22, essendo composto e avendo, quindi, un’altra coppia di fattori risulta essere il prodotto di 2 x 11, dei quali il 2 è inferiore al 5.

Giunto a questo punto ritengo importante sottolineare che al fine della esatta comprensione della distribuzione dei numeri primi utilizzata dalla Natura è di fondamentale importanza avere chiaro l’esatto quadro degli elementi che costituiscono gli intervalli A e B ribadendo che essi corrispondono sempre a elementi consecutivi, detti intervalli limitati e chiusi, i cui estremi corrispondono rispettivamente a:

intervallo A → [n(n-1)+1, n²], rappresentati da [1, 1]; [3, 4]; [7, 9]; [13, 16]; [21, 25]; [31, 36]; ecc.

intervallo B → [n²+1, n(n+1)], rappresentati da [2, 2]; [5, 6]; [10, 12]; [17, 20]; [26, 30]; [37, 42]; ecc.

Analizzando i fattori di cui sono composti i numeri appartenenti a ciascuna linea orizzontale si può notare che ciascun insieme A e B assume una caratteristica costante: osservando il fattore inferiore a n degli elementi presenti negli insiemi A e B si nota che i singoli fattori di ciascun elemento formano una ordinata scala numerica che partendo da 1 arriva fino a n.

Ad esempio, analizzando i fattori dei singoli elementi dell’insieme A di n = 5 si nota che i fattori di 21, 22, 23, 24, 25, sono rispettivamente 3×7, 2×11, 1×23, 4×6, 5×5, dal che si nota che estrapolando da ciascuna di tali coppie di fattori quelli più piccoli si possono ordinare in 1, 2, 3, 4, 5.

21₍₃₎ – 22₍₂₎ – 23₍₁₎ – 24₍₄₎ – 25₍₅₎

Analizzando i fattori dei singoli elementi dell’insieme B dello stesso n=5, si nota che i rispettivi fattori di 26, 27, 28, 29,30 sono rispettivamente 2×13, 3×9, 4×7, 1×29, 5×6, dal che si nota che i fattori più piccoli si possono pure ordinare in 1, 2, 3, 4, 5.

26₍₂₎ – 27₍₃₎ – 28₍₄₎ – 29₍₁₎ – 30₍₅₎

Per ogni insieme A e B si forma sempre e sistematicamente una sequenza di fattori che partendo da 1 (divisore dei primi) giunge fino a n che riflette un altro insieme T composto da una quantità di elementi consecutivi uguale a quello degli insiemi di A e B. Poiché il fattore 1 è caratteristico dei numeri primi, allora si deduce che in ogni insieme A e B si trova sempre un numero primo.

Tale caratteristica degli insiemi non è, però, sempre così lineare come quella descritta per n = 5 (se così fosse, sarebbero stato facile per i matematici accorgersi di tale costante caratteristica) in quanto spesso presenta delle eccezioni che però, a loro volta, si spiegano con ulteriori ragionamenti deduttivi.

Cito qui, per tutti, il caso dell’insieme B di n = 4, costituito dagli elementi 17, 18, 19, 20 dei quali i rispettivi fattori sono 1×17, 2×9, 1×19, 4×5. Qui potrebbe sembrare che il castello teorico finora costruito presenti una falla che inficia la teoria appena espressa in quanto l’insieme di che trattasi è deficiente del fattore 3 e al contempo presenta un doppio fattore 1. Una ulteriore riflessione ci consente però di superare l’ostacolo con l’ausilio della logica matematica. L’elemento 18, oltre che essere costituito dai fattori 1×18, cioè 1 per sé stesso, come tutti i numeri, ed oltre che ad essere costituito dai fattori 2 x 9, è anche costituito dai fattori 3×6. Il processo matematico dei multipli dei numeri, infatti, presenta costantemente elementi aventi confluenze di fattori diversi. In questo caso sul 18 confluiscono il multiplo del 2 e il multiplo del 3. Si noti che sia il 2 che sia il 3 sono fattori inferiori di n=4. Si noti anche che 2 e 3 sono entrambi numeri primi il cui fattore comune è 1. Allora considerando ovvia la casistica dei fattori confluenti su un unico elemento, anche questo insieme B di n = 4, soddisfa la regola che in ogni insieme numerico quadratico A e B, sempre e sistematicamente, si formano una sequenza di fattori inferiori a n ordinabili cronologicamente da 1 fino a n e poiché il fattore 1 è caratteristica esclusiva dei numeri primi, allora si deduce che in ogni insieme A e B si trova sempre almeno un numero primo e che quando gli intervalli sono composti anche da elementi in cui confluiscono divisori minori di n tra di loro primi, allora tali elementi, all’interno dello stesso intervallo diventano, al contempo, causa di un effetto concomitante che si esplica con la presenza di ulteriori numeri primi oltre a quello di base. Infatti, la presenza dell’elemento 18 avente due divisori fra loro primi (2, 3) il cui rispettivo divisore comune è 1 è causa all’interno dello stesso intervallo della doppia presenza di due elementi primi (17, 19) dei quali uno ovvio è l’altro dipendente dalla predetta causa.

Poiché col crescere del valore di n di ciascuna coppia di intervalli aumenta di una unità il numero degli elementi sia dell’insieme A e sia dell’insieme B e poiché aumentano gli elementi degli insiemi A e B aventi fattori diversi da 1, i numeri primi tendono a rarefarsi (poiché all’interno degli insiemi cui appartengono, i fattori dei numeri composti sono sempre più numerosi). Ad esempio, nell’intervallo A di n=11, i cui elementi sono costituiti dagli 11 elementi compresi da 111 a 121,

(111₃ – 112₈ – 113₁ – 114₆ – 115₅ – 116₄ – 117₉ – 118₂ – 119₇ – 120₁₀ – 121₁₁),

avendo ogni elemento un divisore diverso compreso fra 1 e 11, la presenza dei numeri primi si riduce a 1. Al contempo, tuttavia, poiché col crescere del valore di n all’interno degli intervalli cresce anche la presenza degli elementi aventi divisori primi fra loro confluenti, allora tali confluenze, essendo, a determinate condizioni, causa di repliche dei numeri primi, comportano un naturale freno della predetta rarefazione. Infatti, se all’interno degli intervalli quadratici ciascuno degli elementi avesse sempre un diverso divisore Mm così come tendenzialmente capita nei primissimi

intervalli quadratici A (vedere n=1, n=2, n=3, n=4, n=5, n=6, n=10, n=11)

e degli intervalli B

(vedere, n=1, n=2, n=3, n=5, n=7, n=9)

allora la conta dei numeri primi sarebbe estremamente facile riducendosi sempre solo ai 2 compresi fra ciascun quadrato perfetto e il suo successivo. L’altrettanto naturale fenomeno delle confluenze dei divisori Mm (disciplinato da una sere di regole interne comuni a tutti gli intervalli quadratici che stabiliscono quando le confluenze sono causa di repliche di numeri primi e quando no), invece, come anzidetto, comportando un fluttuante aumento di numeri primi interni agli intervalli, i cui temporanei scompensi tendono costantemente a bilanciarsi.

Quando, intorno al 1800, Gauss, con l’ausilio dei logaritmi, riuscì ad elaborare un metodo di quantificazione del costante rapporto di riduzione dei numeri primi rispetto alla totalità dei naturali, inconsapevolmente non fece altro che stabilire la costante connessione tra tali due tendenze contrastanti.

Dalle cronache di letteratura matematica si apprende che inizialmente Gauss non volle rendere nota tale sua scoperta poiché sconoscendo le ragioni della rarefazione dei numeri primi non era certo che la tendenza da lui evidenziata fosse destinata a rimanere fedele anche per le regioni numeriche conosciute. L’obiettivo della successiva ipotesi di Riemann, elaborata nel 1859, infatti, consiste nel riuscire a dimostrare la stima di tendenza che si ricava dal metodo di Gauss. Stima che a tutt’oggi, i calcoli effettuati con l’ausilio della informatica empiricamente confermano, senza tuttavia approdare alla dimostrazione poiché, ignorando la legge matematica che disciplina la distribuzione dei numeri primi, l’edificio matematico rimane carente della conoscenza delle sue fondamenta. Fondamenta che si illumineranno solo quando qualche Università, (scevra da pregiudizi di casta ovvero disponibile ad approfondire l’argomento senza precluderne la possibilità a causa di un mancato allineamento della stesura della teoria al moderno matematichese) vorrà prendere in considerazione e studiare l’articolata proprietà dei numeri naturali (attualmente a loro totalmente ignota) che si annida dentro gli “Intervalli quadratici e divisori Mm, disciplina dei numeri naturali che regola la distribuzione dei numeri primi”.

Pagine 230, formato 21×30, di cui 30 con tabelle a colori, Youcanprint 2024, Euro 29,00

°°°°°°°°°°°°°°°°°°°°°°°°°°°

Per saperne di più cliccare nel sottostante link

https://store.youcanprint.it/sussurri-del-cielo-e-mormorio-di-numeri-primi/b/0756bb96-b947-5fda-becf-2592d2ecf9c6

Il numero 1 è primo? Di più: è un eccezionale primate

Maggio 27, 2024 / filippogiordano

Fra gli argomenti che riguardano i numeri primi periodicamente ritorna una intrigante domanda che gli esperti, con una punta di fastidio, etichettano ingenua: “1 è numero primo?” Generalmente il quesito è posto da semplici appassionati di teoria dei numeri e puntualmente esso appare ozioso a coloro i quali si chiedono una risposta. Oziosa in quanto ha una risposta scontata stante che il teorema fondamentale dell’aritmetica che “Ogni numero naturale maggiore di 1 o è un numero primo o si può esprimere come prodotto di numeri primi”.

Ma fino a quando non si troverà una risposta meno “convenzionale” questa sarà sempre una delle domande principi sui numeri primi poiché se da un lato asserire che 1 ha un solo fattore lascia un margine di dubbio essendo che esso, come i normali numeri primi, ha due fattori (sia pure tra loro uguali) che fra loro moltiplicati conducono al numero stesso (1×3=3, 1×2=2; 1×1=1), dall’altro lato, per convenzione, si distingue e specifica, che sono considerati numeri primi solo quelli che hanno due divisori distinti, escludendo a priori, al fine di evitare problematiche connesse, il numero 1.

Secondo me la divergenza fra chi si pone il dubbio e gli altri può trovare un punto d’incontro, considerando il numero 1 un “eccezionale primo”, ovvero una sorta di primate della evoluzione dei numeri naturali e, in quanto tale, fuori discussione, stante che esso è quantitativamente costituito dalla minima misura in cui possono essere suddivisi tutti gli interi. Sette è 7 volte 1. Cento è 100 volte 1. Uno è misura che tutti, sia primi che composti, catalogano sempre in rapporto alla loro consistenza. Quanti, fra gli altri numeri, a parte sé stessi, hanno solo il divisore 1, sono “etichettati” primi proprio dall’eccezionale 1, in quanto suoi diretti discendenti, ed esso stesso ne garantisce l’autenticità col proprio marchio di esclusivo fattore comune.

Gli altri che, oltre che se stessi e 1, hanno altri fattori, sono numeri composti, discendenti diretti di un qualche coppia di numeri diversa da 1 e da sé stessi, come, ad esempio il 6, prodotto di 2×3, mentre l’altra coppia di divisori (1 e 6) costituisce, il primo (cioè 1) un antenato (ascendente) del secondo (cioè del 6), essendo 2 e 3 a loro volta discendenti dell’1 e al contempo ascendenti del 6. Risulta evidente che sia il 2 che il 3, fattori del 6, entrambi numeri primi, hanno una generazione in meno rispetto a 1, e quindi entrambi non stanno sullo stesso piano generazionale dell’1, essendo quest’ultimo l’archetipo dei numeri, quello che direttamente genera tutti i numeri primi, mentre la diversa sorte di tutti gli altri numeri primi è quella di generare dei numeri composti, come ad esempio il 14, prodotto dai primi 2 e 7, oppure 15, prodotto dai primi 3 e 5.

Ovviamente, sia 14 che 15, come tutti gli altri numeri, a prescindere che siano pari o dispari, hanno pure 1 come loro fattore, tuttavia, nel caso dei numeri composti, 1 è un loro più lontano ascendente, che a essi arriva passando da generazioni numeriche intermedie di numeri primi. Eccezionalmente, infatti, il numero 1, essendo l’archetipo dei numeri, è l’unico dispari ad essere divisore di TUTTI i numeri, compresi i pari.

Essendo l’archetipo dei numeri, 1 ha una primalità essenzialmente diversa da tutti gli altri numeri primi, nel senso che esso si pone al di sopra del concetto di numero primo avente due divisori distinti, stante che esso ne ha sì due, ma fra loro uguali, il cui prodotto conduce allo stesso 1. Figurativamente possiamo pensare che 1 sia il notaio dei numeri naturali interi positivi poiché certifica se essi hanno divisori coincidenti solo con 1 e con sé stessi (oppure sono dei composti) e attribuisce loro la “patente” di numeri primi.

Il numero 1 è eccezionale in quanto primo ed unico numero auto-generatosi (frutto del parto mentale dell’umanità, oppure entità numerica platonicamente esistente nel mondo delle idee universali) mentre tutti gli altri primi sono generati direttamente da esso. Insomma, 1 ha qualità uniche mentre tutti gli altri infiniti numeri primi hanno fra loro la comune proprietà di essere suoi diretti discendenti.

Esistono infiniti numeri primi di forma 6k+1?

Maggio 25, 2024 / filippogiordano

I NUMERI PRIMI DI FORMA 6K+1 SONO INFINITI?

Intorno all’anno 360 a.C. Euclide dimostrò che i numeri primi sono infiniti. È noto che tutti i numeri primi, a parte il 2 e il 3, sono di forma 6k+1 e di forma 6k–1. Ragionevolmente si è portati a considerare che tutti i numeri primi, successivi a quelli noti, siano anch’essi di entrambe le forme possibili 6k-1 e 6k+1, non essendosi riscontrati fra le due predette forme, divergenze tali che possano fare presagire il fatto che a un certo punto del loro infinito percorso lungo il tragitto dei numeri naturali una delle due forme cessi di fornire primi, formando, da quel punto in poi, solo dei numeri composti. Tuttavia, la dimostrazione fornita da Euclide, seppure assicura la infinita presenza di numeri primi, non dimostra che essi lo siano di entrambe le forme oppure che lo siano di una sola forma.

Al fine di effettuare una valutazione esclusiva su ciascuna delle due forme di numeri primi (6k+1 e 6k-1) individuiamo due criteri oggettivi omogenei e verifichiamo l’andamento quantitativo delle presenze di numeri primi al loro interno.

L’analisi dei valori ottenuti dalla differenza dei numeri interi consecutivi positivi elevati al cubo consente di verificare che tali differenze corrispondono sempre a elementi di forma 6k+1 e che, quindi, elencati in ordine progressivo tali differenze, si forma un infinito elenco di numeri di forma 6k+1, fra i quali molteplici numeri primi.

È noto che a parte 2 e 3, tutti i numeri primi sono sempre di forma 6k-1 oppure di forma 6k+1, e che essi quantitativamente si eguaglino lungo la infinita scia dei naturali (5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, di cui i primi sette sono tutti numeri primi). Sebbene l’alternanza fra primi e composti non sia sistematica in quanto man mano che si va avanti i composti di tale forma sono sempre più numerosi dei primi, a lunga distanza la quantità dei numeri primi delle due forme 6k-1 e 6k+1, si equivale e, generalmente, le progressioni di numeri primi ricavabili dalle formule di Eulero sfornano numeri primi di entrambe le forme (ad esempio: 41, 43, 47, 53, 61, 71, 83, ecc…).

Curiosamente la differenza dei numeri naturali interi consecutivi elevati al cubo fornisce sempre e soltanto numeri di forma 6k+1, ovvero numeri eccedenti di una unità i multipli del 6 (…7, 19, 37, 61…).

Differenze delle coppie di numeri consecutivi elevati al cubo

n³– (n-1)³

1³ – 0³ = 1 – 0 = 1;

2³ – 1³ = 8 – 1 = 7;

3³ – 2³ = 27 – 8 = 19;

4³ – 3³ = 64 – 27 = 37;

5³ – 4³ = 125– 64 = 61;

6³ – 5³ = 216 –125 = 91;

7³ – 6³ = 343 –216 = 127;

La sequenza di tali quozienti è matematicamente riassumibile coi valori crescenti di n del polinomio → n(3n-3)+1

Valore di n

1(3×1-3) +1 = 1 x 0 +1 = 1;
2(3×2-3) +1 = 2 x 3 +1 = 7;
3(3×3-3) +1 = 3 x6 +1 = 19;
4(3×4-3) +1= 4 x9 +1 = 37;
5(3×5-3) +1= 5×12 +1 = 61;
6(3×6-3) +1= 6×15 +1 = 91;
7(3×7-3) +1 = 7×18 +1 = 127;
8(3×8-3) +1= 8×21 +1 = 169;
9(3×9-3) +1= 9×24 +1 = 217;
10(3×10-3)+1 =10×27 +1 = 271;

I prodotti dei primi 120 valori di n forniscono 46 numeri primi e sono corrispondenti a poco meno del 40%. Dall’analisi dei numeri ricavabili dalla formula si evince una caratteristica alquanto interessante, cioè che tutti i numeri della sequenza, primi o composti che siano, sono sempre e soltanto di forma 6k+1.

1 → 1 neutro

2 → 7 primo

3 → 19 primo

4 → 37 primo

5 → 61 primo

6 → 91 composto → 7 x 13

7 → 127 primo

8 → 169 composto → 13 x 13

9 → 217 composto → 7 x 31

10→ 271 primo

11→ 331 primo

12→ 397 primo

13→ 469 composto→ 7 x 67

14→ 547 primo

15→ 631 primo

16→ 721 composto→ 7 x 103

17→ 817 composto→ 19 x 43

18→ 919 primo

19→ 1027 composto→ 13 x 79

20→ 1141 composto→ 7 x 163

21→ 1261 composto→ 13 x 97

22→ 1387 composto→ 19 x 73

23→ 1519 composto→ 31 x 49

24→ 1657 primo

25→ 1801 primo

26→ 1951 primo

27→ 2107 composto→ 7 x 301

28→ 2269 primo

29→ 2437 primo

30→ 2611 composto→ 7 x 373

31→ 2791 primo

32→ 2977 composto→ 13 x 229

33→ 3169 primo

34→ 3367 composto→ 7 x 13 x 37

35→ 3571 primo

36→ 3781 composto→ 19 x 199

37→ 3997 composto→ 7 x 571

38→ 4219 primo

39→ 4447 primo

40→ 4681 composto→ 31 x 151

41→ 4921 composto→ 7 x 19 x 37

42→ 5167 primo

43→ 5419 primo

44→ 5677 composto→ 7 x 811

45→ 5941 composto→ 13 x 457

46→ 6211 primo

47→ 6487 composto→ 13 x 499

48→ 6769 composto→ 7 x 967

49→ 7057 primo

50→ 7351 primo

51→ 7651 composto→ 7 x 1093

52→ 7957 composto→ 73 x 109

53→ 8269 primo

54→ 8587 composto→ 31 x 277

55→ 8911 primo

56→ 9241 primo

57→ 9577 composto→ 61 x 157

58→ 9919 composto→ 7 x 13 x 109

59→ 10267 primo

60→ 10621 composto→ 13 x 19 x 43

61→ 10981 composto→ 79 x 139

62→ 11347 composto→ 7 x 1621

63→ 11719 primo

64→ 12097 primo

65→ 12481 composto→ 7 x 1783

66→ 12871 composto→ 61 x 211

67→ 13267 primo

68→ 13669 primo

69→ 14077 composto→ 7 x 2011

70→ 14491 composto→ 43 x 337

71→ 14911 composto→ 13 x 31 x 37

72→ 15337 composto→ 49 x 313

73→ 15769 composto→ 13 x 1213

74→ 16207 composto→ 19 x 853

75→ 16651 primo

76→ 17101 composto→ 7 x 2443

77→ 17557 composto→ 97 x 181

78→ 18019 composto→ 37 x 487

79→ 18487 composto→ 7 x 19 x 139

80→ 18961 composto→ 67 x 283

81→ 19441 primo

82→ 19927 primo

83→ 20419 composto→ 7 x 2917

84→ 20917 composto→ 13 x 1609

85→ 21421 composto→ 31 x 691

86→ 21931 composto→ 91 x 241

87→ 22447 primo

88→ 22969 composto→ 103 x 223

89→ 23497 primo

90→ 24031 composto→ 7 x 3433

91→ 24571 primo

92→ 25117 primo

93→ 25669 composto→ 133 x 193

94→ 26227 primo

95→ 26791 composto→ 73 x 367

96→ 27361 primo

97→ 27937 composto→ 91 x 307

98→ 28519 composto→ 19 x 1501

99→ 29107 composto→ 13 x 2239

100→ 29701 composto→ 7 x 4243 101→ 30301 composto→ 157 x 193

102→ 30907 composto→ 31 x 997

103→ 31519 composto→ 43 x 733

104→ 32137 composto→ 7 x 4591

105→ 32761 composto→ 181 x 181

106→ 33391 primo

107→ 34027 composto→ 7 x 4861

108→ 34669 composto→ 37 x 937

109→ 35317 primo

110→ 35971 composto→ 13 x 2767

111→ 36631 composto→ 7 x 5233

112→ 37297 composto→ 13 x 19 x 151

113→ 37969 composto→ 43 x 883

114→ 38647 composto→ 7 x 5521

115→ 39331 composto→ 37 x 1063

116→ 40021 composto→ 31 x 1291

117→ 40717 composto→ 19 x 2143

118→ 41419 composto→ 7 x 61 x 97

119→ 42127 composto→ 103 x 409

120→ 42841 primo

Nonostante la presenza dei numeri primi all’interno della progressione diminuisca gradualmente, suddividendo la quantità degli elementi della progressione in gruppi di elementi consecutivi di quantità crescenti (1, 2, 3, 4, 5, …) all’interno di ciascun gruppo si osserva la loro costante presenza. Si noti che ciascuna ripartizione così formata si conclude sempre con un numero progressivo corrispondente a un numero triangolare (1, 3, 6, 10, 15, …). Tale criterio uniforme applicato ai primi 120 elementi consente di verificare che nonostante vi siano gruppi che presentano diversi numeri composti consecutivi, ciascuno di essi presenta sempre diversi numeri primi. Il criterio uniforme consente di effettuare delle prove empiriche anche per numeri più grandi, cosicché volendo estendere l’esperimento al gruppo di elementi contenenti il millesimo numero della progressione, considerando che ciascuno dei gruppi di elementi compresi fra un numero triangolare e il suo successivo è normalmente compreso fra n(2n+1)+1 e (n+1)(2n+1), oppure fra n(2n-1) +1 e n(2n+1),

come segue:

1×1 = 1; 1×3= 3;

2×3= 6; 2×5= 10;

3×5= 15; 3×7= 21;

4×7= 28; 4×9= 36;

5×9= 45; 5×11= 55;

6×11= 66; 6×13= 78;

7×13= 91; 7×15= 105,

estraendo la radice quadrata di 1000 si calcola che il millesimo numero progressivo appartiene a un intervallo i cui elementi hanno valori compresi da due fattori dei quali il più piccolo è inferiore e l’altro è superiore alla radice quadrata mentre il rapporto fra i due fattori è approssimato a 1 a 2. Nel caso in esame, infatti i limiti dell’intervallo sono costituiti da 22×45+1 = 991 e 23×45= 1035. Applicando la formula n(3n-3)+1 a ciascuno dei 45 numeri compresi fra 991 e 1035 si ottiene l’intervallo che comprende il millesimo elemento e si rileva se, e in che misura, in tale gruppo sono compresi dei numeri primi.

991→ 2943271 composto→ 19 x 97 x 1597

992→ 2949217 primo

993→ 2955169 composto→ 7 x 67 x 469

994→ 2961127 composto→ 13 x 379 x 601

995→ 2967091 primo

996→ 2973061 composto→ 7 x 13 x 37 x 883

997→ 2979037 composto→ 627 x 1831

998→ 2985019 composto→ 163 x 18313

999→ 2991007 composto→ 157 x 19051

1000→ 2997001 composto→ 7 x 428143

1001→ 3006001 composto→ 43 x 69907

1002→ 3009007 composto→ 1483 x 2029

1003→ 3015019 composto→ 7 x 37 x 11641

1004→ 3021037 composto→ 331 x 9127

1005→ 3027061 composto→ 19 x 159319

1006→ 3033091 composto→ 43 x 70537

1007→ 3039127 composto→ 7 x 13 x 91 x 367

1008→ 3045169 primo

1009→ 3051217 composto→ 13 x 79 x 2971

1010→ 3057271 composto→ 7 x 19 x 127 x 181

1011→ 3063331 composto→ 13 x 9787

1012→ 3069397 primo

1013→ 3075469 composto→ 643 x 4783

1014→ 3081547 composto→ 7 x 440221

1015→ 3087631 composto→ 31 x 103 x 967

1016→ 3093721 composto→ 43 x 71947

1017→ 3099817 composto→ 7 x 442831

1018→ 3105919 composto→ 67 x 151 x 307

1019→ 3112027 composto→ 757 x 4111

1020→ 3118141 composto→ 13 x 239857

1021→ 3124261 composto→ 7 x 446323

1022→ 3130387 composto→ 13 x 240799

1023→ 3136519 composto→ 127 x 24697

1024→ 3142657 composto→ 7 x 19 x 23629

1025→ 3148801 primo

1026→ 3154951 composto→ 751 x 4201

1027→ 3161107 primo

1028→ 3167269 composto→ 7 x 223 x 2029

1029→ 3173437 composto→ 19 x 167023

1030→ 3179611 primo

1031→ 3185791 composto→ 7 x 199 x 2287

1032→ 3191977 composto→ 31 x 102967

1033→ 3198169 composto→ 13 x 37 x 61 x 109

1035→ 3210571 composto→ 7 x 13 x 35281

L’uniforme criterio di ripartizione dei progressivi elementi ricavati dalla formula generale che ripartisce quantità sempre maggiori di numeri di forma 6k+1 per ciascun gruppo, assicura la ciclica presenza di elementi i quali sono multipli di piccoli divisori che si vanno alternando con altri che hanno divisori sempre più grandi e altri ancora sprovvisti di divisori maggiori di 1, ovvero numeri primi. Tanto perché se da un lato cresce la presenza di elementi composti aventi fattori più grandi, dall’altro lato il ciclo di ricomparsa di ulteriori elementi composti aventi medesimi fattori più grandi si estende a maggiori quantità di elementi intermedi e in tali elementi intermedi si annidano sempre elementi numeri primi non scomponibili da fattori diversi da 1.

Questa progressione di numeri naturali positivi tutti di forma 6k+1, suddivisa in gruppi formati da intervalli di elementi quantitativamente crescenti tutti contenenti al loro interno molteplici numeri primi, fa presupporre che i numeri primi di tale forma siano infiniti. Sono del parere che quando i numeri naturali, incanalati dentro alcuni modelli matematici, assumono caratteristiche costanti e uniformi, conservino perpetuamente tali loro abitudini, tuttavia, consapevole che in matematica il parere non assume testimonianza di certezza, la presente resta al momento solo una supposizione, ovvero una mera congettura.

Terne pitagoriche

Maggio 6, 2024 / filippogiordano

Una formula con m, n, entrambi dispari

alternativa a quella di Euclide

È noto che per terna pitagorica s’intende una terna di numeri naturali a, b, c, tali che a²+b²=c². Il nome proviene dal famoso teorema di Pitagora che afferma “la somma dei quadrati perfetti costruiti sui cateti di ogni triangolo rettangolo con lati interi è equivalente al quadrato perfetto costruito sull’ipotenusa”. Il fatto che esistono infinite terne pitagoriche è stato dimostrato da Euclide nei suoi Elementi il quale ha fornito la formula in grado di trovare tutte le terne pitagoriche:

con m>n,

a= m² – n²;

b= 2mn;

c= m² + n².

Per la realizzazione delle terne occorre comunque distinguere che attribuendo sia a m che a n valori alternativi dispari, pari, (ad esempio m=7, b=4) oppure pari, dispari, (ad esempio m=5, n=4) a condizione che m ed n siano coprimi, cioè senza divisori comuni, allora si ottengono delle terne pitagoriche primitive, mentre, invece, se m ed n hanno dei divisori comuni (esempio: m=12 ed n=9) oppure se m, n sono entrambi dispari oppure entrambi pari si ottengono delle terne pitagoriche derivate.

Da quanto premesso sembrerebbe che la possibilità di ottenere terne primitive sia ottenibile soltanto abbinando valori alternativi pari/dispari o dispari/pari ad M e N, così come indicato dalla equazione di Euclide.

Incuriosito da ciò ho fatto una ricerca sul web per verificare se esistono formule alternative che consentono di trovare terne pitagoriche primitive assegnando entrambi valori dispari sia a M che N senza trovarne traccia, probabilmente perché, considerata l’indiscussa autorità di Euclide, a nessun matematico è mai venuto in mente di valutare la possibilità di trovare un percorso alternativo. Potrebbe pure darsi che qualcuno abbia trovato qualcosa in merito e che però si tratti di qualcosa di affatto noto e per questo non rintracciabile sui vari siti internet che descrivono le terne pitagoriche. Fatto sta che neanche sulla pagina dedicata di Wikipedia si trova qualcosa in merito.

Cimentandomi a fare alcune prove in tale direzione ho trovato che esiste almeno una formula che consente di ottenere a sua volta tutte le infinite possibilità di terne pitagoriche primitive assegnando sia a M che a N valori esclusivamente dispari. La stessa formula, inoltre consente di aggiungere una ulteriore tipologia di terne (ma di tale aspetto mi soffermo in coda alla esposizione).

Infatti, con m ed n entrambi numeri dispari ed m>n, assegnando ad

a= mn;

b = [(n²-m²)/2]

c = [(n²+m²)/2]

allora, con m ed n coprimi, a²+b²=c² è sempre una terna pitagorica primitiva, salvo che m ed n non siano coprimi e, quindi, abbiano fra loro divisori in comune.

A tal proposito, a titolo esemplificativo, coi primi valori di m ed n, ho predisposto alcune delle infinite tabelle realizzabili. Ciascuna di tali tabelle, estensibile all’infinito, raggruppando gli abbinamenti di uguale differenza fra m ed n, (la prima con differenza 2, la seconda con differenza 4, la terza con differenza 6, ecc.) rappresenta solo i primi valori di una serie infinita, diversa da ciascuna delle altre, ed è ovvio che essendo infinite le distanze possibili fra m ed n, infinite sono pure le serie realizzabili.

Così come la formula generale fornita da Euclide è valida per ciascuna serie (mano a mano diversificandosi in dipendenza degli infiniti valori attribuibili a m ed n) anche la formula da me trovata resta sempre utilizzabile per ciascuna serie. Inoltre, così come succede per le infinite serie euclidee, anche in questo caso ciascuna serie è distinguibile con una distinta formula singolarmente applicabile a quella sola serie. E’ altrettanto ovvio che così come è diversa la formula generale, diverse sono anche le formule relative a ciascuna delle serie. Nel caso specifico, ciascuna delle formule relative alle diverse serie è trascritta in calce alla tabella di pertinenza.

L’elaborazione delle strutture delle formule mi ha consentito di notare una caratteristica costante delle terne pitagoriche che è quella che ciascuna terna pitagorica, sempre formata da tre distinti numeri a, b, c, elevati al quadrato, ha una perpetua relazione con un invisibile quarto elemento quadratico il quale stabilisce rapporti di connessione fra esso e ciascuno degli elementi che costituiscono la terna stessa.

Al fine di procedere gradualmente nella disamina dell’argomento proposto, prima di evidenziare tale connessione ritengo però opportuno mostrare le prime otto delle infinite tabelline citate, ciascuna delle quali contiene in alto la formula generale in grado di generare tutte le infinite serie, e in basso quelle singolari che si riferiscono alla sola serie delle infinite terne ricavabili da ciascuna tabella.

tabella 1

valore m	valore n	a= mn;	b = [(m²-n²)/2]	c = [(m²+n²)/2].
3	1	3	4	5
5	3	15	8	17
7	5	35	12	37
9	7	63	16	65
11	9	99	20	101
13	11	143	24	145
15	13	195	28	197
17	15	255	32	257
19	17	323	36	325
21	19	399	40	401
23	21	483	44	485
25	23	575	48	577
27	25	675	52	677
29	27	783	56	785
31	29	899	60	901
33	31	1023	64	1025

tabella 2

valore m	valore n	a= mn;	b = [(m²-n²)/2]	c = [(m²+n²)/2].
5	1	5	12	13
7	3	21	20	29
9	5	45	28	53
11	7	77	36	85
13	9	117	44	125
15	11	165	52	173
17	13	221	60	229
19	15	285	68	293
21	17	357	76	365
23	19	437	84	445
25	21	525	92	533
27	23	621	100	629
29	25	725	108	733
31	27	837	116	845
33	29	957	124	965

diverse altre analoghe tabelle e diversi altri articoli visualizzabili al libro di cui al seguente link

https://store.youcanprint.it/quaterne-quadratiche-terne-pitagoriche-primi-gemelli/b/b407a9b2-0e96-5e8d-9861-7021acf891a6

Monografia sul tema Primi di Mersenne e numeri perfetti — dav

Radice numerica dei numeri perfetti

Maggio 4, 2024 / filippogiordano

(da: “Primi di Mersenne e numeri perfetti”)

Accanto a un misterioso infinito planetario c’è un infinito numerico anch’esso pieno di misteri che, dagli albori della ragione, ha calamitato l’attenzione dell’uomo caricandolo di molti interrogativi.

Numeri primi e numeri perfetti hanno sempre esercitato un fascino particolare sia sui luminari della matematica che sui dilettanti. È la irregolarità della loro distribuzione a carpire l’attenzione. Il desiderio di mettere ordine all’apparente caos. Geni come Pitagora ed Euclide, dilettanti (così loro amavano definirsi) come Fermat e Goldbach, luminari come Eulero e Gauss, hanno fermato la loro attenzione su tali concatenazioni asimmetriche.

Perfino poeti–filosofi come Eratostene e monaci, come Mersenne, hanno dedicato parte della loro vita al problema numeri primi e numeri perfetti lasciando una marcata impronta. A quest’ultimo appartiene l’idea di estrapolare dalla formula di Euclide la parte connotativa di alcuni primi che costituiscono il fattore principe per la ricerca dei “perfetti”, numeri che, negli ultimi 70 anni, sono stati oggetto di una intensificata ricerca da parte di alcune università americane, le quali hanno scandagliato una serie molto vasta di numeri mastodontici alla ricerca di questi aghi nel pagliaio, riuscendo a scoprirne, dal 1952 al 1999, grazie all’ausilio della informatica, ben 27 che vanno ad accrescere la esigua lista dei 12 precedentemente scoperti nel corso di 2500 anni e ad aggiungerne ulteriori 10 dal 1999 ad oggi.

Gli ultimi perfetti scoperti sono numeri colossali, ciascuno dei quali è formato da milioni di cifre, comprensibili alla mente umana solo se espressi in forma ridotta, ovvero sotto forma di potenze.

Seppure, presi singolarmente, siano perfettamente inutili, cioè senza alcun valore pratico, (ovvero utili soltanto alla crittografia che da oltre un trentennio li utilizza per messaggi cifrati) la ricerca dei numeri primi di Mersenne e dei corrispondenti numeri perfetti continua con la speranza che una volta o l’altra qualcuno riesca a decifrare la loro sequenza irregolare e che riesca a risolvere i dubbi che arrovellano i matematici. I numeri perfetti sono infiniti? Si troverà un metodo veloce che consenta la loro individuazione?

Dopo essermi dedicato alla interpretazione della dinamica che determina i numeri primi con la ricerca che ho titolato “Perfetto 6, il file nascosto dei numeri primi” , pubblicata nel maggio 2001, l’angelo della curiosità ha spinto il molto dilettante matematico che è in me a mettere il naso nel campo dei “numeri perfetti” per averne un quadro il più possibile completo. Ne ho scrutato, quindi, i più reconditi meandri , ho voltato e risvoltato tutti gli aspetti conosciuti tentando di andare oltre le attuali conoscenze, aggiungendo, nel corso dell’anno 2003, un piccolo contributo alla causa riuscendo a svelare uno dei tanti quesiti che l’argomento pone, ovvero come e perché la radice numerica dei numeri perfetti è sempre uguale a 1. Soluzione allora successivamente avvalorata dal fatto che il teorema, inizialmente pubblicato on line in un sito di matematica, venne integralmente ripreso e inserito in una tesina di una studentessa della Facoltà di Matematica della Università di Torino durante l’anno accademico 2004-2005, tesina successivamente pubblicata integralmente nello spazio online della Uni.To riservato alla docente.

Tanto, ovviamente non vuol dire che non si percepiscano le reali distanze culturali tra il professionismo e il dilettantismo. Resta però la convinzione che alcune strade possano essere percorse con efficacia anche dal dilettante, il quale avendo la testa sgombra dai cliché accademici può intraprendere percorsi di matematica elementare non precedentemente esplorati essendovi, contrariamente alla attuale credenza dei matematici, ancora diverse primitive strade ignote, in grado di allacciare relazioni fra argomenti messi a fuoco da alcuni grandi del passato ma non ulteriormente indagati dai loro successori.

A me, che da molti anni percorro i sentieri della poesia, piace pensare a questa ricerca come ad una sorta di poemetto che racconta una storia originariamente piena di punti oscuri che, poco alla volta, vengono focalizzati come nodi di un aggrovigliato gomitolo, colorando di nuova luce la storia primitiva dei numeri.

NUMERI PRIMI, COMPOSTI, DIFETTIVI, ECCEDENTI E PERFETTI

Secondo la scuola pitagorica, in matematica si definiscono primi quei numeri che sono divisibili solo per se stessi e per il numero 1, mentre tutti gli altri numeri interi sono definiti composti perché originati dal prodotto di 2 o più numeri primi. I numeri composti, a loro volta, si dividono in eccedenti, difettivi e perfetti. Tale differenziazione dei composti dipende dai divisori.

Difettivi: quando la somma dei divisori di un numero è minore del numero stesso quel numero è definito difettivo. I divisori del 15, ad esempio, sono 1, 3 e 5 che addizionati fra loro, danno come somma 9.

Eccedenti: quando la somma dei divisori di un numero è maggiore del numero stesso, quel numero è definito eccedente. I divisori del 12, ad esempio, sono 1, 2, 3, 4 e 6, che addizionati fra loro danno come somma 16.

Perfetti: quando la somma dei divisori di un numero è uguale al numero stesso, quel numero è definito perfetto. Il numero 6, che ha come divisori 1, 2 e 3, è, di conseguenza, un numero perfetto.

Nella scala dei numeri naturali si incontrano quasi sempre difettivi e composti. Raramente, invece, si incontrano i perfetti. Perché la peculiarità della perfezione appartiene a pochissimi numeri. Basti pensare che fino alla ragguardevole cifra di 33.550.336. si incontrano solo 5 numeri perfetti. Per trovare il sesto numero dobbiamo arrivare a 8.589.869.056.

Fu Pitagora ad accorgersi che i numeri perfetti oltre ad essere la somma di tutti i loro divisori sono anche la somma di una serie di numeri naturali consecutivi. Ad esempio:

06	=	1 + 2 + 3,
28	=	1 + 2 + 3 + 4 + 5 + 6 + 7
496	=	1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +…+ 30 + 31,
8.128	=	1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +…+ 126 + 127,
33.550.336	=	1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +…+ 8.190 + 8.191.

Successivamente Pitagora annotò che le potenze del 2 conservano la caratteristica di essere numeri lievemente difettivi, non perfetti a causa del costante scarto minimo di una sola unità:

2²	=	(2*2)	=	4	Divisori	1,2,	Somma	3,
2³	=	(222)	=	8	Divisori	1,2,4,	Somma	7,
2⁴	=	(222*2)	=	16	Divisori	1,2,4,8,	Somma	15,
2⁵	=	(22222)	=	32	Divisori	1,2,4,8,16,	Somma	31,
2⁶	=	(22222*2)	=	64	Divisori	1,2,4,8,16,32,	Somma	63,
2⁷	=	(2222222)	=	128	Divisori	1,2,4,8,16,32,64,	Somma	127,
2⁸	=	(2222222*2)	=	256	Divisori	1,2,4,8,16,32,64,128,	Somma	255,
2⁹	=	(222222222)	=	512	Divisori	1,2,4,8,16,32,64,128,256,	Somma	511,
2¹⁰	=	(222222222*2)	=	1.024	Divisori	1,2,4,8,16,32,64,128,256,512,	Somma	1.023.

Fu Euclide a stabilire, successivamente, la relazione istituita da Pitagora tra il due e la perfezione, scoprendo che i numeri perfetti sono sempre multipli di due numeri, uno dei quali è una potenza di due e l’altro è la successiva potenza di 2 meno 1.

6	=	2¹ x (2² – 1)
28	=	2² x (2³ – 1)
496	=	2⁴ x (2⁵ – 1)
8128	=	2⁶ x (2⁷ – 1)

Oggi i computer hanno continuato la ricerca dei numeri perfetti e hanno trovato esempi di numeri colossali che obbediscono alla regola d’Euclide.

I numeri perfetti finora scoperti sono più di 50, il più grande dei quali ha 49 724 095 cifre. I primi quattro possono essere scritti nel modo seguente:

2 x 3 cioè	2 x (4 – 1),
4 x 7 “	4 x (8 – 1),
16 x 31 “	16 x (32 – 1),
64 x 127 “	64 x (128 –1).

Evidenziando le potenze del 2 presenti in ogni numero perfetto, Euclide, nel 300 a. C., diede la formula dei numeri perfetti, nei suoi Elementi, Libro 9, Proposizione 36:

se p è un numero primo e, a sua volta 2^p – 1 è sempre primo, allora 2^{p – 1} (2 ^p – 1) è un numero perfetto.

LA FORMULA DI MERSENNE

Uno dei due fattori della formula dei numeri perfetti di Euclide (2^p – 1) diede l’idea a Marin Mersenne, frate minimo francese vissuto a Parigi dal 1588 al 1648, di ricercare quei particolari numeri che costituiscono il supporto primario dei numeri perfetti. Quindi è sufficiente trovare un numero primo di Mersenne per avere anche, collegato a questo, un nuovo numero perfetto.

Mersenne, nella prefazione alla sua Cogitata Physico Mathematica, affermò che 2^p–1 è primo per p= 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257 e per nessun’altro numero p minore di 257. Tale affermazione si è però rivelata inesatta in quanto Frank Nelson Cole, nel 1903, scoprì che 2⁶⁷-1 non è primo e successivamente anche 2²⁵⁷–1 non lo è. Inoltre, altri esponenti inferiori a 257, danno luogo a numeri primi: p= 61, 89, 107.

Dal 2001 ad oggi sono stati scoperti altri 12 primi di Mersenne. Gli ultimi numeri scoperti sono colossali. Essi contano milioni di cifre. Per scrivere il 38 numero perfetto, ad esempio, occorre un volume con diverse centinaia di pagine: esso è costituito da ben 4.197.919 cifre ed è più comprensibile se così espresso:

2^6972592(2^6972593-1).

Roba che soltanto i computers possono gestire. Tuttavia la ricerca procede spedita, grazie ad una fondazione americana, la GIMPS (The Great Internet Mersenne Prime Search – La Grande Ricerca Internet di Numeri Primi di Mersenne) che è collegata con diverse migliaia di amatori sparsi nel mondo ciascuno dei quali, coi loro piccoli computers, scandagliano una fetta numerica. La fondazione distribuisce un premio di 100.000 dollari a ciascuno dei fortunati che ha la ventura di imbeccare la fetta numerica che contiene l’ennesimo primo di Mersenne. Gli ultimi 17 numeri colossali sono stati scoperti grazie alla GIMPS.

Si intuisce che una volta avviato il meccanismo, il computer debba restare in funzione per diverso tempo. Si dice che il giapponese che ha scoperto uno degli ultimi (in ordine di tempo) numero perfetto abbia fatto lavorare il proprio per oltre 100 giorni consecutivi.

Man mano che la ricerca è andata avanti è stato verificato anche un altro aspetto riguardante le cifre dei numeri perfetti maggiori di 6 finora scoperti: sommando ciascun elemento della cifra di un numero perfetto, si ottiene un numero le cui cifre sommate tra loro convergono nel numero uno. Sommando, ad esempio, gli elementi del numero 28 si ha che 2+8=10 e quindi 1+0= 1. Il risultato finale della somma degli elementi di ciascun numero si suole definire radice numerica.

Ad esempio:

Numero perfetto	Radice Numerica
6,	= 1
28,	= 1
496,	= 1
8128,	= 1
33550336,	= 1
8589869056,	= 1
137438691328,	= 1
2305843008139952128,	= 1
2658455991569831744654692615953842176	= 1

Man mano che la ricerca sui numeri perfetti è andata avanti è stata notata una loro curiosa proprietà: la somma delle singole cifre di cui è composto ciascun numero (ad eccezione del 6), perpetuata fino al raggiungimento di una sola cifra, converge sempre a 1. Ad esempio, sommando le singole cifre del quarto numero perfetto (8128) si ha che 8+1+2+8 = 19; a sua volta 1+9 = 10; infine, 1+0 = 1.

Tale caratteristica ha indotto i ricercatori ad avanzare l’ipotesi che tutti i numeri perfetti, compresi quelli ancora ignoti, conservino tale proprietà. Tuttavia, fin quando tale congettura è rimasta non dimostrata, ogni dubbio sulla sua veridicità era legittimo nonché avvalorato dalla diversità del primo numero perfetto (il perfetto 6 che, per l’appunto, ha radice numerica = 6). Dubbi e perplessità che coincidevano con i seguenti interrogativi:

Per quale motivo il primo perfetto non collima con la radice 1? Esso costituisce l’unica eccezione oppure, in seguito, se ne scopriranno altre? Lo squarcio di luce che illumina la congettura proviene da una riflessione che (così come per la congettura di Teone di Smirne riguardante la cifra finale dei perfetti sempre uguale a 6 oppure 8) trova spiegazione nelle dimensioni cicliche dei sistemi numerici.

Teorema:

Ad eccezione del 6,

CIASCUN NUMERO PERFETTO HA SEMPRE RADICE NUMERICA UGUALE a 1

Euclide, nel 300 avanti Cristo osservò che con n = numero primo, ogni qualvolta 2ⁿ-1 corrisponde a sua volta ad un ulteriore numero primo, allora 2^n-1(2ⁿ-1) è un numero perfetto.

Aumentando gradualmente il valore di n della formula euclidea, da 1 all’infinito, si ottengono infiniti cicli esa-numerici, ciascuno dei quali contiene al suo interno, numeri che rispettivamente confluiscono nelle seguenti radici: 1, 6, 1, 3, 1, 9.

2^n-1 (2ⁿ –1)	prodotto	radice numerica

(2^1-1)(2¹ –1)	1	1
(2^2-1) x (2² –1)	6	6
(2^3-1) x (2³ –1)	28	1
(2^4-1) x (2⁴ –1)	120	3
(2^5-1) x (2⁵ –1)	496	1
(2^6-1) x (2⁶ –1)	2016	9

(2^7-1) (2⁷ –1)	8128	1
(2^8-1) (2⁸ –1)	32640	6
(2^9-1) (2⁹ –1)	130816	1
(2^10-1)(2¹⁰–1)	523776	3
(2^11-1) (2¹¹–1)	2096128	1
(2^12-1) (2¹²–1)	8386560	9

(2^13-1) (2¹³ –1)	33550336	1
(2^14-1) (2¹⁴ –1)	134209536	6
(2^15-1) (2¹⁵ –1)	536854528	1
(2^16-1)(2¹⁶–1)	2147450880	3
(2^17-1) (2¹⁷–1)	8589869056	1
(2^18-1) (2¹⁸–1)	34359607296	9

–

E così via, all’infinito.

Nell’ambito dei primi 2 cicli esa-numerici della formula euclidea sopra riportati si incontrano i primi 4 numeri perfetti, determinati da n avente valore uguale ai numeri primi 2, 3, 5 e 7.

Si può notare che tutti i numeri corrispondenti a valore di n dispari hanno radice numerica 1, mentre tutti quelli corrispondenti a valore di n pari hanno, alternativamente, radice numerica del 3 e dei suoi multipli (6-3-9).

Il 6 (unico fra i numeri perfetti ad avere radice numerica diversa da 1) infatti, è il prodotto dei due fattori aventi l’unico esponente n primo pari, cioè il 2: 2^2-1(2²-1) = 2×3 = 6.

Poiché condizione necessaria e indispensabile affinché 2ⁿ-1 sia un numero primo è quella, preliminare, che n corrisponda ad un numero primo e poiché tutti i numeri primi, ad eccezione del 2, sono dispari, allora tutti i numeri perfetti poiché determinati dalla formula euclidea avente n uguale = numero dispari conservano sempre (ad eccezione di n = 2) la radice numerica 1.

——————–

Ulteriori informazioni sui numeri perfetti possono essere assunte nel libro ottenibile collegandosi al seguente link

https://store.youcanprint.it/primi-di-mersenne-e-numeri-perfetti/b/2dc62ecf-f7f7-5f10-864c-7d683f7e4d8f